k nearest neighbors

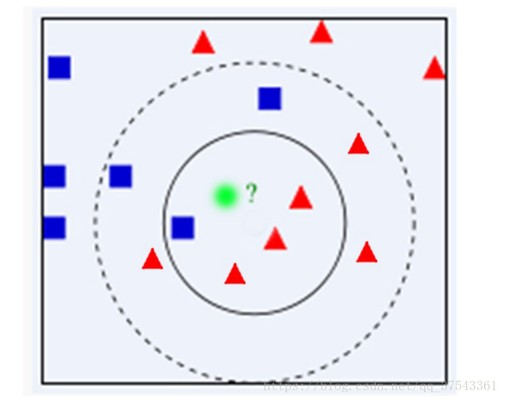
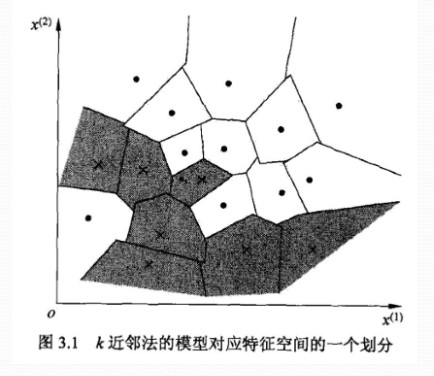
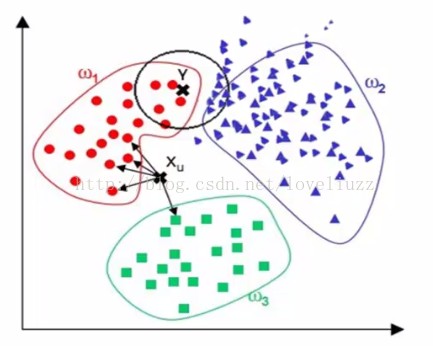
kNN算法简介: kNN(kNearestNeighbors)算法又叫k最临近方法,总体来说kNN算法是相对 比较容易理解的算法之一,假设每一个类包含多个样本信息,而且每个信息都有 一个唯一的类标记表示这些样本是属于哪一个分类,kNN就是计算每个样本数 据到待分类信息的距离,取和待分类信息最近的k各样本信息,那么这个k个样 本信息中哪个类别的样本信息占多数,则待分类信息就属于该类别。 基于kNN算法的思想,我们必须找出使用该算法的突破点,本文的目的是使用 kNN算法对文本进行分类,那么和之前的文章一样,关键还是项向量的比较难题, 之前的文章中的分类代码仅使用的反余弦来匹配

文章浏览阅读1.9k次。前一阵子,在学习机器学习参考资料《Machine learning in action》,一本以python语言为主。python比较简单,写算法比较灵活,对数组矩阵的计算形式调用较为简单。第一个机器学习的例子,就是kNN,它是一个简单的机器学习模型,容易理解而且效率高。原理和它的想法都很简单:用距离来分类的方法,计算待分类样例与已知所有分类样例的距离,对影响进行排序,找出最小距离的前_nearestneighbors原理 学习消息历史k-Nearest Neighbors(KNN)算法—原理篇 https://blog.csdn.net/qianmeiling2848/article/details/51124505版权机器学习和python专栏收录该内容3 篇文章

K-nearest Neighbors 学习方法是基于实例的,可用于逼近实值或离散目标函数,概念简明。对于基于实例的算法,学习过程只是简单地存储已知的训练信息,当遇到新的查询实例时,一系列相似的实例被从存储器中取出,并用来分类新的查询实例。所以,基于实例的算法的最大不足也就在于分类新实例的开销特别大。 关于该算法的基本介绍可以参考下教材或是维基百科。这里主要写一下比较关键的难题。 k-nearest neighbor algorithm对于K-nearest Neighbors算法而言,其距离是根据标准欧式距离定义的。可以把实例看做为一个多维向量,其距离就是求向量间的距离。 1NN:预测值或类别,仅

文章浏览阅读5.4k次,点赞2次,收藏8次。KNN最近邻算法是一种基于实例的学习,通过计算新样本与已知分类样本的距离,选择最近的K个样本,以多数类别决定新样本的分类。本文详细介绍了KNN的步骤、特点、距离计算方法、K值选择以及K折交叉验证,并提供了代码示例。 学习C 知道 消息历史KNN最近邻算法(K - Nearest Neighbors) 版权KNN最近邻算法是一种基于实例的学习,通过计算新样本与已知分类样本的距离,选择最近的K个样本,以多数类别决定新样本的分类。本文详细介绍了KNN的步骤、特点、距离计算方法、K值选择以及K折交叉验证,并提供了代码示例。 KNN最近邻算

k 近邻法(K-Nearest Neighbors Algorithm,k-NN)是一种基本分类与回归方法,通过多数表决等方式进行预测,所以不具有显式的学习过程。 k 近邻算法 输入:训练信息集 ,其中 是实例的特征向量, 是实例的类别, ;实例特征向量 ; 输出:实例 所属的类 根据给定的距离度量,在训练集 中找出与 最近邻的 个点,涵盖这 点的 的邻域记作 ; 在 中根据分类决策规则决定 的类别 : k 近邻模型 k 近邻法使用的模型实际上对应于特征空间的划分。模型由三个基本要素——距离度量、k值的选择和分类决策规则决定。 特征空间中,对每个训练实例点 ,距离该点比其他点更近的所有点组成一个区域,叫做单元。下

文章浏览阅读2.3w次,点赞4次,收藏32次。邻近算法,或者说K最邻近(KNN,K-NearestNeighbors)分类算法是分类方法中最简单的方法之一。所谓K最近邻,就是K个最近的邻居的意思,说的是每个样本都可以用它最接近的K个邻近值来代表。近邻算法就是将信息集合中每一个记录进行分类的方法。KNN 最初由 Cover 和 Hart 于1968年提出,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。_k-nearest neighbors 【机器学习】K近邻算法(K-NearestNeighbors , KNN)详解 + Java代码达成 于 2023-01-09 08:05:48 首次发布 https://blog.csdn.net/weixin_51545953/article/details/128

版权机器学习专栏收录该内容38 篇文章 1、简介 (1)Cover和Hart在1968年提出最初的临近算法 (2)邻近算法属于分类(classification)算法 (3)输入基于实例的学习(instance-based learing),懒惰学习(lazy learing)——应对训练集时并没有建造任何的模型,当对一个未知的实例进行归类时才进行归类 2、举例 如何将电影的例子模拟成一个广泛的模型? 对于每一个电影模拟成一个实例点,每个点的特征向量(在这里是二维的),可以是N维的,即:每个点都可以抽象成空间中具有多维的空间向量。 每个点所对应的标签分类的值是我们的目标

作为一个非参数学习算法,k-nearest neighbors能够达成非常高的容量(capacity)。例如,我们有一个多分类任务,使用0-1损失函数来衡量性能。在这样的设定下,1-nearest neighbor在训练样本接近无穷大时收敛到2倍贝叶斯误差。多出来的贝叶斯误差来自随机在两个距离相同的邻居里选一个。当有无穷多训练信息时,所有测试点x\pmb{x}xxx都会有无穷多邻接距离为0。如果算法被允许在这些邻居上投票,而不是随机选择一个,则该过程会收敛到贝叶斯误差率。k-nearest neighbors的高容量使我们在给定一个大型训练集能够取得高准确度。它以高计算量达成这点,不过,给定一个小的有限的数

训练集X \pmb{X}XXXy \pmb{y}y​y​​yy ^ = y i \hat{y}=y_iy^​=yi​i = a r g m i n ∣ ∣ X i , : − x ∣ ∣ 2 2 i=argmin||\pmb{X_{i,:}-x}||_2^2i=argmin∣∣Xi,:​−x​Xi,:​−x​​Xi,:​−x∣∣22​L 2 L^2L2X i ; : X_{i;:}Xi;:​y i y_iyi​信息集更一般的,k-nearest neighbors是一类可以被实践于分类或者回归的技术。作为一个非参数学习算法,k-nearest neighbors不受限于固定数量的参数。我们通常认为k-nearest neighbors算法没有任何参数,而是达成了一个训练信息的简单函数。事实上,甚至不需要一个训练阶段或者学习过程。取而代之的是,在测试时,当我们需要为一个新的测试输入x \pmb

k-nearest-neighbors:k-近邻分类算法在MNIST数字信息集上的达成.一、K -近邻算法(KNN:k-Nearest Neighbors) 版权一、K -近邻算法(KNN:k-Nearest Neighbors) 算法基本思想:物以类聚,人以群分 存在一个样本信息集合,也称作训练样本集,并且样本集中每个信息都存在标签。输入没有标签的新信息后,将新信息的每个特征与样本集中信息对应的特征进行比较,随后算法提取样本集中特征最相似信息(最相邻)的分类标签。一般